Thought I’d do something different and run a little competition with the chance of winning a copy of my book. It’s based on one of the learning exercises we give to our students on our Masters in Clinical Gait Analysis by distance learning If you’ve got students, trainees or junior colleagues maybe you’d like to forward the URL of this post to them so that they can have a go. Our students enjoy the exercise and I assume they will too. They also learn a lot about how we walk and how to measure the ground reaction.
This exercise requires students to experiment with walking in different ways to modify the characteristics of the ground reaction. You can download a full description here. First of all they are simply asked to walk at different speeds and record the ground reaction. They then compare the data with those in Mike Schwartz’s paper on how gait patterns in general vary with walking speed. Generally there is good agreement but occasionally we’ll find someone who doesn’t vary speed in the same way that the average person does (whoever that is!).
Then I give them a number of different graphs of theoretical ground reactions and ask them to try and walk in such a way that they match the shape of the graph. The two below, for example, are to walk with exaggerated peaks of the vertical component and then with a flat pattern.
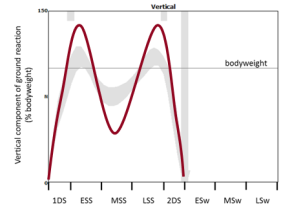
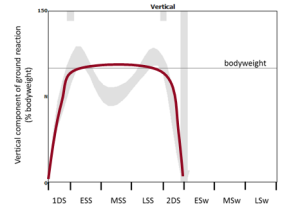
The students generally find these reasonably easy. The more alert ones spot that the flat pattern is simply what you get if you walk slowly but it can be reproduced in a normal speed walk if you think about what you are doing..
Then come two more – one with the first peak higher than the second and finally the second peak higher than the first.


Again the first is easy. It is what happens if you walk faster (but like the flat peaks there are also ways of recreating it at normal speed). The second is much harder and so far (over two years now) none of the students has come up with a convincing example of walking with a higher second peak than first.
This interests me because a few years ago Barry Meadows and some of his colleagues published a paper based on their observation that in patients with a wide range pathologies you almost always find that the second peak of the ground reaction is diminished – never the opposite. They called this Ben Lomonding, after a mountain in Scotland that has two peaks – one of which is higher than the other.

So I just wonder – is it possible to walk in this way? I’m prepared to offer a copy of my book (signed of course!) for the person who can provide the best version of the fourth graph above (2nd ground reaction considerably higher than the first) as real ground reaction data.
Part of the aim of the learning exercise is for students to think about the relationship between the ground reaction and the movement of the centre of mass and we ask them to explain how they have changed their walking pattern in order to alter the ground reaction.
I suspect it will be a lot easier if you adopt a highly asymmetrical pattern or adjust your gait for the particular step when you hit the force plate. I’ll be more much more impressed if you can illustrate the phenomenon with a symmetrical, repeatable gait pattern.
I’ll use these last two criteria (convincing explanation, and repeatability and symmetry of gait) to judge the winner in the event that more than one person comes up with a solution.
Maybe we need a few rules. Two weeks feels like about the right time. Send entries to me (r.j.baker@salford.ac.uk) by midnight (UK time) on Monday 29th February. They should include:
- a graph of the vertical component of the ground reaction (you might want to include the GRF from both legs if you want to impress me with your symmetry)
- a video of you walking over the force plate (or you could send a link to one you’ve uploaded to YouTube of Vimeo or somewhere else publicly accessible – this is what I encourage our students to do). These are particularly useful if you can overlay the ground reaction vector but I won’t insist on this as a lot of people still don’t have the technology (if all you’ve got is a smart phone then use that). Try and capture at least one step before and one step after the measurement if you want to impress me with the repeatability of your gait pattern).
- a biomechanical explanation of how you have changed your walking pattern in order to change the ground reaction in this way.
To ensure that entries are genuine I will be try to replicate the best entries in my lab here on the basis of the explanations provided. If I can’t do this I may ask for proof that the data is real (e.g. data in a .c3d other file format that has obviously come directly from a force plate).
I’ll assume that in submitting these you’ll be happy for me to use the graphs and video in a future post reporting the results. (Note that I won’t publish the explanations – I feel people should be free to write what they want without fear that it will get posted publicly).
Finally, if you enjoy the exercise and would like to engage more, why not think about enrolling on the Masters programme. You can do it as part time study in your current workplace and do not need to travel to Salford at all. You can find details at this link.


