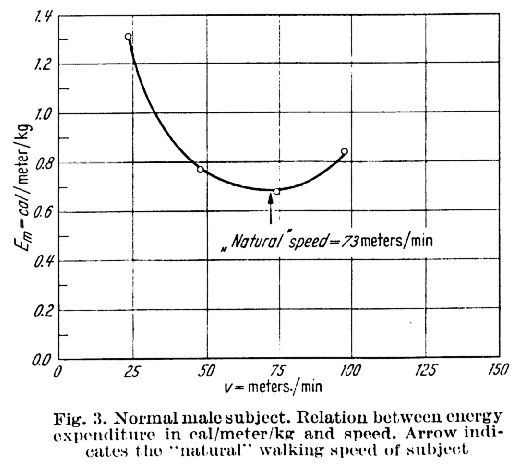
Sheila from Dundee dropped me an e-mail:
In your meanderings around the subject of gait have you come across any definitive descriptions of push-off i.e. at what time in the cycle does it start? Or do you have any thoughts on the matter yourself?
Having replied it struck me that others may be interested in this topic.
As far as I’m aware “push-off” is only used loosely to describe a phase of the gait cycle. I’ve never seen a definition in terms of where it starts and where it ends. My preference is to describe the phases based on single and double support and swing (with single support and swing divided into three equal parts). This intentionally avoids labelling any particular phase as having any particular function (push-off, shock-absorption etc.) partly because people often get these functions wrong when describing walking and partly because patients may not achieve such functions at the same phase of the gait cycle as the able-bodied.
“Push-off” is particularly problematic. How usefully it describes the late stance phase depends both on whether you are considering the whole body or just the leg and the direction you are talking about. During late stance the centre of mass is moving downwards and forwards. The downward motion is being resisted. From this perspective late stance is a phase of deceleration and the term “push-off” is inappropriate. The segments in the limb however are moving in different directions, the foot, ankle and tibia are being “pushed up” whereas the femur is actually moving downwards with the centre of mass.
Looking in the horizontal direction both the centre of mass and the limb are being accelerated forwards. There is a relatively small acceleration of the centre of mass (but this affects a large mass) and a rapid acceleration of the limb (which has a much smaller mass). In this context “push-off” does appear an appropriate descriptor at first.
Focussing first on the centre of mass movement though – if you model the whole body as an inverted pendulum with mass and leg length matching the human body you find that the entirely passive mechanism (no muscle activity) develops an anterior component of a ground reaction in late stance that is very similar in magnitude to that of the ground reaction at this phase of healthy walking. This force arises because of the relative alignment of the centre of mass, limb and foot and suggests that the muscles need only preserve this alignment to generate it. “Push-off” suggests something much more active and may be misleading.
If we focus on the limb – there has been a debate for nearly 200 years about whether it is being pushed forwards by the action of the plantarflexors pushing against the ground or pulled forwards by the hip flexors. I think it very likely that both are important. It’s tempting to think that some insight into this can be gained from looking as the joint power graphs. They show power generation at both hip and ankle which tends to confirm that both are important. Power, however, is a scalar quantity (it is not associated with any particular direction) representing the rate at which energy is supplied to or removed from the whole body by the muscles acting across a particular joint. Given this it is very difficult to come to any rigorous conclusions about the relationship between the power generated at the joints and the movement in a particular direction of the segments of the limb being “pushed-off” (to say nothing of complications when power may actually be being generated by muscles spanning more than one joint). To answer the problem categorically would require some form of induced acceleration analysis as to what particular muscles are acting to accelerate the segments during late stance. I’m not aware of anyone having done this (perhaps readers can let me know if they are).
Going back to the original question. I’d maintain my suggestion that we avoid “push-off” as a term. It’s an easy label to apply that makes us think we understand something that many of us don’t (and I’d include myself in this).